1. 準ニュートン法とは
1.1 はじめに
高速に局所的最適解を求められる古典的手法です。
「準」と付いている通り,その更新式はニュートン法の式を準えています。
1.2 ニュートン法の原理
![]()
上の無制約最適化問題の最小値は、最適性の条件式(微分した関数が0)で与えられる。
![]()
上式を解くために,xからsだけ移動した点x+sを考え,
![]()
が成り立つようなsを与えるために,上の式をxで1次近似すると,
![]()
となる.移動量は、
![]()
と与えられる.これによって,ニュートン法のモデル
![]()
が得られる.
以下の図は,∇f(x)に初期値xを与えて接線を引き,xを更新して解に近づいていくのを図示したもの.
図だと、分かりやすい!
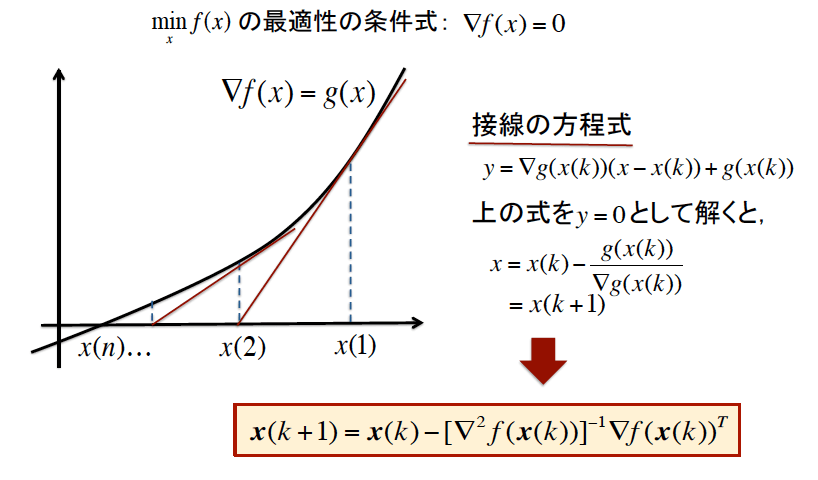
1.3 準ニュートン法とは
しかし、上で説明したニュートン法には、実用手法として以下のような問題点があります。
- ヘッセ行列∇^2f(x)の計算が容易でない場合がある
- ヘッセ行列∇^2f(x)が正則でなく、逆行列が存在しない場合がある
準ニュートン法は、ニュートン法のヘッセ行列を近似するものです。 更新式はこちら。
![]()
ニュートン法のヘッセ行列の逆行列を近似する公式に、今回は以下のDFP公式を用います。
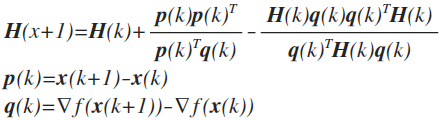
1.4 コード
実際の2次元でのコードは、こちら。(このレポジトリで管理してます。)
直線探索には、黄金分割法を用いました。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
#include <iostream>
#include <fstream>
#include <math.h>
using namespace std;
#define N 2
#define K 1000
#define EPS 0.01
#define eps 0.001
double __2n_minima (double x1, double x2);
void gold (double *x1, double *x2, double dx1, double dx2);
int main()
{
double x[N];
int count = 0;
char filepath[256];
sprintf(filepath, "run/gold.txt");
ofstream fout; // file出力の為の定義
fout.open(filepath); // fileを開く
fout << "#m\tstate\tx1\tx2" << endl; // 見出し出力
for (int m = 1; m <= 100; m++) {
bool flag = false;
for (int n = 0; n < N; n++) {
x[n] = ((double)rand() / ((double)RAND_MAX + 1)) * 10 - 5;
}
double y[N], f[N], z[N];
double p[N], q[N];
double dx1, dx2, norm;
// 近似行列の初期値は、単位行列
double j11 = 1, j12 = 0, j21 = 0, j22 = 1;
double g11 = 0, g12 = 0, g21 = 0, g22 = 0;
for (int k = 0; k < K; k++) {
for (int n = 0; n < N; n++) {
z[n] = f[n];
f[n] = 4 * pow(x[n], 3) - 32 * x[n] + 5;
}
if (k != 0) {
norm = sqrt(dx1 * dx1 + dx2 * dx2);
if(norm < EPS) {
flag = true;
break;
}
for (int n = 0; n < N; n++) {
p[n] = x[n] - y[n];
q[n] = f[n] - z[n];
}
g11 = p[0]*p[0] / (p[0]*q[0]+p[1]*q[1]) - ((j11*q[0]+j21*q[1]) * (j11*q[0]+j12*q[1])) / (q[0]*(q[0]*j11+q[1]*j21) + q[1]*(q[0]*j12+q[1]*j22));
g12 = p[0]*p[1] / (p[0]*q[0]+p[1]*q[1]) - ((j12*q[0]+j22*q[1]) * (j11*q[0]+j12*q[1])) / (q[0]*(q[0]*j11+q[1]*j21) + q[1]*(q[0]*j12+q[1]*j22));
g21 = p[1]*p[0] / (p[0]*q[0]+p[1]*q[1]) - ((j11*q[0]+j21*q[1]) * (j21*q[0]+j22*q[1])) / (q[0]*(q[0]*j11+q[1]*j21) + q[1]*(q[0]*j12+q[1]*j22));
g22 = p[1]*p[1] / (p[0]*q[0]+p[1]*q[1]) - ((j12*q[0]+j22*q[1]) * (j21*q[0]+j22*q[1])) / (q[0]*(q[0]*j11+q[1]*j21) + q[1]*(q[0]*j12+q[1]*j22));
}
if (p[0] * f[0] + p[1] * f[1] < 0) {
// Hesseの近似行列の各成分
j11 = j11 + g11;
j12 = j12 + g12;
j21 = j21 + g21;
j22 = j22 + g22;
} else {
// 単位行列にリセット
j11 = j22 = 1;
j12 = j21 = 0;
}
dx1 = j11 * f[0] + j12 * f[1];
dx2 = j21 * f[0] + j22 * f[1];
for (int n = 0; n < N; n++) {
y[n] = x[n];
}
gold (&x[0], &x[1], dx1, dx2);
}
char state[256];
if (flag) {
sprintf(state, "収束");
} else {
sprintf(state, "なし");
}
fout << m << "\t";
fout << state << "\t";
fout << x[0] << "\t";
fout << x[1] << endl;
double tmp_gbest = __2n_minima(x[0], x[1]);
if (tmp_gbest <= -150) {
count++;
}
}
fout << count << endl;
return 0;
}
// 目的関数
double __2n_minima (double x1, double x2)
{
double f;
f = pow(x1, 4) - 16 * pow(x1, 2) + 5 * x1 + pow(x2, 4) - 16 * pow(x2, 2) + 5 * x2;
return f;
}
// 黄金分割法
void gold (double *x1, double *x2, double dx1, double dx2)
{
double x1_max, x2_max, a, b, f1, f2;
int count = 0;
double tau = (sqrt(5) - 1) / 2;
double norm = sqrt(dx1*dx1 + dx2*dx2);
dx1 = dx1 / norm, dx2 = dx2 / norm;
x1_max = *x1 - dx1, x2_max = *x2 - dx2;
while (count < 100) {
count += 1;
a = __2n_minima(*x1, *x2);
b = __2n_minima(x1_max, x2_max);
f1 = __2n_minima(*x1 - (1-tau) * dx1, *x2 - (1-tau) * dx2);
f2 = __2n_minima(*x1 - tau * dx1, *x2 - tau * dx2);
if (f1 < f2) {
x1_max = *x1 - tau * dx1;
x2_max = *x2 - tau * dx2;
} else {
*x1 = *x1 - (1 - tau) * dx1;
*x2 = *x2 - (1 - tau) * dx2;
}
dx1 = *x1 - x1_max;
dx2 = *x2 - x2_max;
norm = sqrt(dx1*dx1 + dx2*dx2);
if (norm < eps) break;
}
f1 = __2n_minima(*x1 - (1-tau) * dx1, *x2 - (1-tau) * dx2);
f2 = __2n_minima(*x1 - tau * dx1, *x2 - tau * dx2);
if (f1 < f2) {
*x1 = *x1 - (1-tau) * dx1;
*x2 = *x2 - (1-tau) * dx2;
} else {
*x1 = *x1 - tau * dx1;
*x2 = *x2 - tau * dx2;
}
}